This article is part of a series entitled Language Games. See also:
1. Wild Grammar; 2. Combinatorial Grammar; 3. Pragmatic Grammar
“All doors will not open.” — operator, Amtrak Northeast Regional train, Charlottesville
In language, scope ambiguities are one of the trickiest parts of semantic theory. Semantic meaning is famously said to be determined compositionally: the meaning of a larger sentence is determined by the meanings of its smaller parts, as well as by the way these smaller parts are assembled into a whole. Even so, there can be interactions between these parts, in the sense that certain words can exert control over other words. When one word influences how another is interpreted, it is said to hold that word in its scope.
For example:
Every king admires himself. [2]
In this situation, the reflexive pronoun himself is given meaning by the separate noun king, which holds himself in its scope.
Let’s consider another example:
Puck didn’t solve one problem. [2]
What does this mean? It actually depends on how scope is assigned. It’s ambiguous. Indeed, this sentence, due to Fromkin, et. al. [2] (with paraphrases partially my own), carries two distinct meanings:
- Puck didn’t solve one problem.
- It is not the case that Puck solved one problem. He solved none, or perhaps two or three.
- There is one particular problem that Puck didn’t solve. He may have solved other problems, though, perhaps even exactly one other problem.
The key difference here, as we’ll see, is whether the scope of the negation contains, or does not contain, one problem.
In this article, following the pattern of the last, I’ll begin by exploring some examples of delightful scope ambiguities I’ve come across in the literature. I’ll also attempt to explain some of the delicate theory surrounding these constructions. In the second part, we’ll play some games.
I’ll begin with an important technical point. The possible scope readings permissible to a sentence can be constrained by so-called c-command relations. Roughly speaking, one word is said to c-command another when the syntax subtree formed by taking the first word’s parent node as root contains the second word. Words higher in the syntax tree tend to c-command words lower in the tree. For example, in
Puck didn’t solve one problem,
the negation not c-commands the noun phrase one problem.
In a scope ambiguity involving two words with the property that one c-commands the other, one of the two scope readings is held to be more natural than the other. Indeed, the reading in which the c-commanding word outscopes the other is called the linear, or surface scope reading; the opposite reading is called the inverse scope reading. We’ll soon see that an inverse scope reading is not always permissible.
The precise meaning of the word outscope – that is, what scope means at all – is best understood when one writes a sentence’s various meanings in first-order logic. First, one should rather try to grasp this meaning intuitively. Later, we’ll see precise logic at work.
Negation and determiner phrase
Many scope ambiguities, like Puck’s above, involve interchanging the scope of a negation with that of a determiner phrase. Consider the following two examples (and paraphrases), again by Fromkin [2]:
- “Richard III didn’t murder fewer than three squires.”
- “It is not the case that Richard III murdered fewer than three squires; he murdered at least three squires.”
- *”There are fewer than three squires whom R. III didn’t murder.”
- “Fewer than three squires didn’t obey Richard III.”
- *”It is not the case that fewer than three squires obeyed R. III; at least three squires obeyed him.”
- “There are fewer than three squires who didn’t obey R. III.”
In sentences 2 and 3, the negation alternates in scope with the determiner phrase fewer than three squires.
In sentence 2, the surface scope reading is that in which not outscopes fewer than three; in sentence 3, the surface scope reading is that in which fewer than three outscopes not. (This can be seen by observing the sentences’ syntax trees.) Fromkin, et. al. place stars next to paraphrases 2.B. and 3.A., indicating that the meanings suggested by these paraphrases — the inverse scope readings — aren’t actually furnished by the English language. Indeed, some scope ambiguities aren’t really ambiguous in the sense that the alternate (in this case the inverse) among two meanings is so ridiculous that no English speaker would acknowledge it as legitimate.
Fromkin, et. al [2] provide a sophisticated account of the circumstances under which an inverse scope reading is permissible. (In this case, it has to do with the so-called decreasingness of the determiner fewer than three [2].) The literature only takes this further (I can only offer the excellent paper [3]). While this question is rich and fascinating, I won’t take it up. My interest lies not so much in which readings are acceptable to English speakers as in how many readings we can create, acceptable or not. We’ll see more of this in the second part.
In the sentence “All doors will not open”, above, the hapless train operator utters a sentence in which the inverse scope reading is the intended one. (We hope.)
Verb and determiner phrase
A second class of scope ambiguities I’ve found seems to involve, roughly, the interchanging of the scopes of a determiner and a verb. I lack the sophistication required to describe this class adequately; I only refer the reader to Park [3]. Consider the following sentence, adapted from a sentence originally due to Hendriks (1993) and considered by Park [3]:
Fred believes that a mathematician wrote “Through the looking glass.”
I’ll offer paraphrases. For the reader’s benefit, I’ll also attempt to write each scope reading in first-order logic.
- Fred believes that a mathematician wrote “Through the looking glass.”
- believe(F, ∃u[math(u) ∧ write(u, L)])
According to Fred’s belief, there exists some mathematician such that that this mathematician wrote “Through the looking glass.” - ∃u[math(u) ∧ believe(F, write(u, L))]
There exists some person, a mathematician, such that Fred believes that this person wrote “Through the looking glass.”
- believe(F, ∃u[math(u) ∧ write(u, L)])
In the second scope reading, the determiner phrase a mathematician attains inverse scope over the verb believes.
These readings don’t in fact amount to the same thing. Reading 4.A. could be true while 4.B. remained false, if, say, the mathematician featured in Fred’s belief did not really exist. On the other hand, if, say, Fred believed that a certain person wrote “Through the looking glass” while failing to realize that this person was a mathematician, then reading 4.B. would be true while reading 4.A. remained false.
I’ll offer another, and slightly subtler, example. Consider the following sentence, again adapted from Park [3]:
Fred claims that every schoolboy is intelligent.
I’ll offer paraphrases and first-order logic expressions:
- Fred claims that every schoolboy is intelligent.
- claim(F, ∀v[boy(v) → intelligent(v)])
According to Fred’s claim, each schoolboy is intelligent. - ∀v[boy(v) → claim(F, intelligent(v))]
For each schoolboy which exists, Fred claims that this schoolboy is intelligent.
- claim(F, ∀v[boy(v) → intelligent(v)])
In the second reading, the determiner phrase every schoolboy attains inverse scope over the verb claims. These readings are also independent from each other, a fact whose details I’ll leave to the reader.
Two or more determiner phrases
A large class of scope ambiguities arises from interchanging the scopes of two determiner phrases in some sentence. Consider the following example and paraphrases, from Fromkin [2]:
- “Two fairies have talked with every Athenian.”
- “There are two fairies such that each has talked with every Athenian.”
- “For every Athenian, there are two possibly different fairies who have talked with him/her.”
Here, the determiner phrase two fairies c-commands the determiner phrase every Athenian, and yet the two phrases freely alternate in scope. Sentence 6.B. paraphrases the inverse scope reading. These sentences don’t amount to the same thing. Sentence 6.B. could be true while sentence 6.B. remained false, if, say, each Athenian were visited by both members of precisely one among a collection of pairwise disjoint pairs of fairies. In that case, (using the surface scope reading) no fairies would have talked with every Athenian.
Sentences with two statements of quantity can behave in analogous ways:
Three Frenchmen visited five Russians. [3]
Barring the so-called cumulative reading — under which this sentence would be true of an encounter which took place between two groups (see the comments to this piece) — this sentence has two standard, ambiguous scope readings. This readings are also semantically independent of each other, in the above sense that one can construct situations for which any one holds true while the other does not. For example, consider the following two situations:
- Three Frenchmen visited five Russians.
- There exist three Frenchmen such that each of these three Frenchmen visited each member of precisely one among three pairwise disjoint collections of five Russians.
- Each member of a collection of five Russians was visited by each member of precisely one among five pairwise disjoint collections of three Frenchmen.
In situation 7.A., the surface scope reading holds while the inverse reading does not; in situation 7.B., the inverse scope reading holds while the surface scope reading does not.
Park studies still wilder examples. In the following sentences, collected by Park, three distinct determiner phrases compete for scope. Park, and those he cites, claim that not all possible readings are available in English (see the comments above). Nonetheless, the number becomes quite high.
- Every representative of a company saw most samples.
- Some student will investigate two dialects of every language. [3]
Very generally, it appears that a sentence containing multiple determiner phrases must assemble these phrases into one among the many possible partial orders admissible on them. This is to say that in any logical expression representing such a sentence, the relation outscopes defines a reflexive, transitive, and anti-symmetric relation on the set of all determiner phrases. There are a number of such orderings on any nontrivial set.
In common language, this means that in any scope reading of a sentence containing multiple determiner phrases, while certain pairs of determiner phrases might be such that one outscopes the other, there may be other pairs whose elements are parallel, or between which no relation exists. (We can call such determiner phrases incomparable.) We will see examples of this below.
I’ve been unable to find, in the literature, corroboration for the possibility that a sentence’s scope ordering may represent a partial, as opposed to a total, order. Perhaps the examples I present below get something wrong.
In any case, this situation presents a number of difficulties. For one, we must be prepared to ask which of a sentence’s possible readings (that is, partial orders) are available in the English, in the sense discussed by Park. A further difficulty arises. Among the available readings, which are independent, in the sense of freedom from semantic entailment described above? Certain readings will resist the construction of situations for which that reading holds and no others do.
Games
I’ll now see how far I can stretch English’s capacity to bear scope ambiguities. As I’ve mentioned, I will not seek to determine which of a sentence’s scope readings are practically comprehensible as English interpretations (most of them won’t be). I’m interested only in whether they logically represent meanings of the sentence.
Game 1: Construct a family of sentences 1, …, n, … such that the nth sentence has n+1 mutually independent scope readings.
Solution: Consider a collection of people P1, P2, …, Pn, … and the family of sentences:
- A mathematician wrote “Through the looking glass.”
- P1 believes that a mathematician wrote “Through the looking glass.”
- P2 believes that P1 believes that a mathematician wrote “Through the looking glass.”
…
- Pn believes that … P2 believes that P1 believes that a mathematician wrote “Through the looking glass.”
This set of sentences exploits the verb and determiner phrase class of scope ambiguities, which I’ve found particularly amenable to linear growth. In short, in any given member of this family the determiner phrase “a mathematician” gradually escapes from a nested set of beliefs and into reality (see also Park [3], pp. 27-28). For the sake of example, I’ll offer first-order logic expressions for each of sentence 3’s three possible scope readings:
- P2 believes that P1 believes that a mathematician wrote “Through the looking glass.”
- believe(P2, believe(P1, ∃u[math(u) ∧ write(u, L)]))
- believe(P2, ∃u[math(u) ∧ believe(P1, write(u, L))])
- ∃u[math(u) ∧ believe(P2, believe(P1, write(u, L)))]
Each of this family’s sentences’ various scope readings are semantically independent. Consider an arbitrary sentence n and order its n+1 scope readings by preservation of c-command relations, as above, and pick an arbitrary scope reading, say the ith one. I’ll prove that this ith reading implies no others.
For this, it will suffice to construct a situation about which this ith scope reading, and none of the others, holds, and this I’ll do now. I’ll use a trick of notation to make the proof’s explication more elegant: I’ll use the nonsensical “P(n+1) believes” to mean “it is true that”. Suppose now that this ith scope reading’s logical expression is true, in the sense that we have a nested chain of beliefs from Pn+1, …, P1 according to which, in particular, Pi believes that the person present in P1‘s belief is a mathematician. Suppose now in addition that, again according to this nested chain of beliefs, the Pj for j < i fail to acknowledge that this believed writer is a mathematician that the Pj for j > i do not believe that this mathematician exists. In this intricate situation, the ith reading holds and none of the others do.
Game 2: Construct a family of sentences 1, …, n, … such that the nth sentence has 2n mutually independent scope readings.
Solution: Consider a collection of disjoint groups of people A1, B1, A2, B2, …, An, Bn, … and the following sentences:
- Two A1s visited two B1s.
- Two A1s visited two B1s and two A2s visited two B2s.
…
- Two A1s visited two B1s and two A2s visited two B2s and … two Ans visited two Bns.
This family operates through a somewhat trivial n-wise conjunction of clauses which each, individually, feature a two-way scope ambiguity. Each among sentence n‘s n clauses may, independently, take either surface or inverted scope. There are as many scope readings as there are binary sequences of n digits.
This family also boasts the property that each of its sentences’ scope readings are independent. Indeed, consider a sentence n and an arbitrary scope reading d represented, say, by the n binary digits d1, … , dn. To construct a situation in which this and no other scope reading holds, we must simply suppose that something like 7.A. applies to all those groups Ai, Bi such that di = 0 and something like 7.B. applies to all those groups Ai, Bi such that di = 1 (for all i = 1, …, n). In such a situation, clearly d holds; conversely, any different reading d’ = d’1, … , d’n where di ≠ d’i, say, fails to hold because its failure on the individual pair Ai, Bi takes down the whole conjunction.
There is no scope relation between the determiner phrases two Ais and two Ajs for i ≠ j. These phrases, in other words, are incomparable. Though this behavior is interesting, it’s achieved in a somewhat trivial way. To distinguish this phenomenon from a more interesting sort, we’ll say that two determiner phrases in a given scope reading are non-trivially incomparable if, between them, no scope relation exists and yet a c-command relation does exist.
Game 3: Construct a family of sentences 1, …, n, …, such that the nth sentence features “complicated behavior” loosely defined—such as the presence of many independent scope readings, themselves featuring many non-trivially incomparable pairs.
Solution: Consider a collection of disjoint groups of people G1, G2, …, Gn, … and the following sentences (with embeddings bracketed to resolve syntactic ambiguity):
- There are exactly two G1s.
- There are exactly two G2s [who talked to exactly two G1s].
…
- There are exactly two Gns [who talked to exactly two G(n-1)s [ … [who talked to exactly two G1s] … ]].
In pursuit of the somewhat contrived task put forward by this game, I’ll undertake to characterize the scope readings available to the the arbitrary sentence n indicated above. This characterization will proceed in several stages.
Recall from the above that each scope reading available in a given sentence corresponds uniquely to a partial order on the set of that sentence’s determiner phrases; the set of all such partial orders in turn is in one-to-one correspondence with set of all graphs with nodes the sentence’s determiner phrases which are directed acyclic and transitively reduced. Associating to each determiner phrase exactly two Gks the node , we thus must characterize sentence n‘s scope readings among the directed acyclic transitively reduced graphs on the n vertices
. I’ll begin with an inductive characterization:
Claim 1 (Inductive characterization of admissible scope readings). The graphs associated to sentence n‘s scope readings are characterized among the directed acyclic transitively reduced graphs on n vertices as exactly those
which can be built using the following inductive process:
- Define
- Define
by setting
and then following exactly one of the following two procedures:
- Set
- Set
- Set
Set .
Briefly, the placeholder variable r keeps track of what we may think of as the tree’s root node; at each stage, we may either append a new root or build upon a chain of nodes trailing from the existing root.
Proof. These steps clearly generate directed acyclic transitively reduced graphs. There are now two things to show here: That each generated graph represents an admissible scope reading, and that these are the only such.
The idea is essentially, again, an inductive one. I’ll take for granted here the perhaps subtle fact that sentence n is given meaning—and its scope ambiguities resolved—in an “inside-out” manner (in other words, its syntax tree is semantically analyzed using a bottom-up traversal). The content of the claim, then, is that the noun phrase
exactly two Gks who talked to exactly two G(k-1)s … who talked to exactly two G1s.
can be given meaning only by inductively giving meaning to
exactly two G(k-1)s … who talked to exactly two G1s.
and then using exactly one of the following two procedures:
- Let exactly two Gks outscope the entire noun phrase exactly two G(k-1)s … who talked to exactly two G1s.
- Let exactly two Gks be outscoped by the single determiner phrase exactly two G(k-1)s.
That these modifications are sound (the first implication above) is essentially a linguistic fact, and must be proven “by linguistic intuition”: all I can do is provide examples. That the opposite implication holds—and these are the only acceptable steps—is again a consequence of the bottom-up semantic analysis of a sentence: any other steps would intercede within the existing phrase, which has already been given meaning in the bottom-up traversal.
For example, let’s consider in particular the sentence 3:
- There are exactly two G3s [who talked to exactly two G2s [who talked to exactly two G1s]].
Claim 1 is powerful enough for us to exhaustively characterize the scope readings of sentence 3. In the following diagram, I display the directed acyclic transitively reduced graph corresponding to each of this sentence’s 4 scope readings. Under each graph, I describe a situation under which that graph’s scope reading is true and none of the others are. As a visual aid, in this diagram and those that follow, edges adjoined using procedure A. above will be drawn horizontally and to the left, while edges adjoined using procedure B. above will be drawn upwards and to the left.
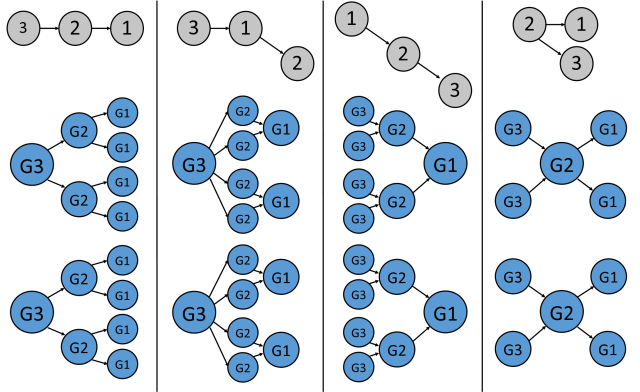
Sentence 3 admits four independent scope readings.
Interestingly, the fourth panel above exhibits our first instance of non-trivial incomparability (between nodes 1 and 3). We will discuss this more below.
For further visual aid, I’ll indicate a few of the admissible scope readings on a graph with 10 nodes. Here, I just provide the scope graphs:
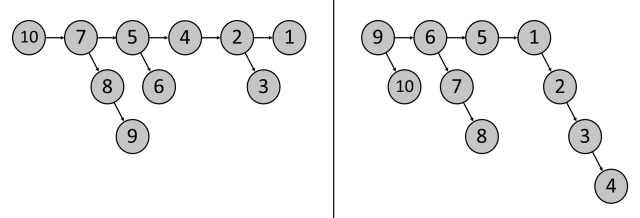
These graphs represent two of the scope readings of sentence 10, all of which are arborescences.
That Claim 1 describes all and only the acceptable scope readings is, at the end of the day, a matter of linguistic intution—I don’t have the tools to say more!
It may be of interest, now, to characterize the graphs generated by Claim 1 among the directed acyclic transitively reduced graphs on n nodes in a way that is not inductive, but employs instead a “closed form”: a set of conditions that one may explicitly test on any given graph. This closed form is given below.
I’ll write to signify that
and
are connected by an edge, and I’ll write
to indicate that there exists a path from node
to node
. We now have:
Claim 2 (Closed form characterization of admissible scope readings). A directed acyclic transitively reduced graph on n vertices
is generated using the inductive procedure of Claim 1, and thus represents an available scope reading of sentence n, if and only if it is connected and in addition satisfies each of the following three conditions:
- If
for nodes
, then the boolean expression
is true.
- If
for nodes
for which
, then
.
- Every node is covered by at most one other node.
One can check, for example, that the graphs in the diagrams above satisfy these conditions.
Proof. Since you’ve made it this far, I may once again disappoint you here. I have in fact taken the pains to prove this theorem myself. The proof, on the other hand, was an immense, and fairly tedious, exercise in subdividing into cases and manipulating boolean expressions. If somebody bothers to deem this work valuable, then I will be happy to write out a rigorous proof!
In the mean time, I will make a few statements. The forward direction of this proof (Claim 1 → Claim 2) is easier; it involves simply demonstrating that the inductive procedures of Claim 1 preserve the conditions of Claim 2. Note first that the base case (, a graph with one node and no arrows) clearly satisfies the conditions of Claim 2. One must then show that, provided
satisfies the claim’s conditions,
does too. This itself involves handling the options k. A. and k. B. separately; for each such option, the conditions 1., 2., and 3. of Claim 3 must be verified independently. (This is not very hard to do.)
The opposite implication is trickier. We must show that any graph not constructible using the procedures of Claim 1 is either disconnected or fails to satisfy at least one of the conditions of Claim 2. My idea here is to use a sort of converse induction. Fix a directed acyclic transitively reduced graph on the nodes
which is not constructible using the procedures of Claim 1. Note first G can be assembled in a step-by-step procedure whereby on step k the node
is added together with all of the edges in the sets
and
. Moreover, on at least one of these steps, the edges added must fail to conform to the requirements of Claim 1, or else G would be generable using these procedures after all. It’s enough to show, then, that if our graph violates Claim 1’s procedures at any one of these stages, the ultimate graph G must fail at least one of the conditions of Claim 2. This involves a fair amount of sophisticated checking, and I will set aside that task here.
These sentences satisfy the loosely defined conditions put forth by Game 3. For one, fairly many of the partial orders on n elements are of the form specified by Claim 2—exactly 2n-1 of them, it would seem, as appending each non-initial node represents a choice between exactly two options. We have thus provided a second, and roundabout, solution to Game 2. (Counting the overall number of partial orders on n elements is much harder). Meanwhile, as c-command relations obtain between all the determiner phrases in sentence n, in any admissible partial order any two nodes between which no order relation exists are non-trivially incomparable—and of these, too, there are many. The analogous fact was not true of our first solution to Game 2.
It would be interesting, of course, to establish more general results regarding the availability of scope readings—for instance, to formulate a general procedure whereby an arbitrary syntax tree is mapped onto the set of its admissible scope readings. In particular, one could discover sentences for which a great many possible scope readings obtain among its determiner phrases, or for which few obtain.
This suggests:
Game 4: Construct a family of sentences 1, …, n, …, such that the nth sentence has n determiner phrases among which all, or many, or few (or no?) scope orderings are available.
Any ideas?
- Kripke, Speaker’s Reference and Semantic Reference
- Fromkin, et. al. Linguistics: An Introduction to Linguistic Theory
- Jong C. Park. Quantifier Scope, Lexical Semantics, and Surface Structure Constituency
To keep the below comments comprehensible, I’ll preserve here my old treatment of Game 3. (I’ve artificially advanced the date of this comment to place it on top.) What follows has, by now, been all but discredited. See the article, and the more recent comments below, for the updated treatment.
Game 3: Construct a family of sentences 1, …, n, … such that the nth sentence has n! mutually independent scope readings.
Incomplete solution: Consider a collection of disjoint groups of people G1, G2, …, Gn, … and the following sentences (with embeddings bracketed to resolve syntactic ambiguity):
1. There are exactly two G1s.
2. There are exactly two G2s [who talked to exactly two G1s].
…
n. There are exactly two Gns [ … [who talked to exactly two G2s [who talked to exactly two G1s]] … ].
I hoped, in this family, to construct sentences n each containing n distinct determiner phrases — the phrases exactly two Gis, for i = 1, …, n — among which all n! scope orderings could obtain. Unfortunately, these sentences appear not to meet this goal. The goal posed by this game is quite difficult, and I haven’t yet been able to satisfactorily meet it.
This family offers a partial solution. As we’ll see, only some of the n! possible scope orderings — those of a very particular sort, in fact — will convey sensible meanings. The failing, furthermore, might reflect an intrinsic limitation of language itself. Let’s begin.
As a matter of notation, for any given sentence n and for each i = 1, …, n, I’ll denote the determiner exactly two attached to the noun phrase Gi simply by the number i. I’ll also use the greater-than sign > to denote outscoping. In this way, I will be able to concisely encode any of this sentence’s scope readings. The surface scope reading, for example, would be denoted by n > … > 2 > 1.
Let’s understand what these sentences (can) mean. As a first non-trivial example, we’ll take sentence 2:
2. There are exactly two G2s [who talked to exactly two G1s].
The following diagram depicts respective scenarios in which precisely one of the two possible scope readings holds.

Indeed, the left-hand diagram depicts a situation in which the surface scope reading 2 > 1 holds and the inverse reading does not; the right-hand side depicts a situation in which the inverse scope reading 1 > 2 holds and the surface reading does not. We see, therefore, that the two scope readings of sentence two are both coherent and independent. It should be noted that there are many other situations for which one of these statements may hold, including many which hold for both (imagine, for example, two G2s and two G1s such that every G2 connects to every G1). I’ve chosen these situations precisely because they hold for just one.
Read the sentence while looking at each of these two diagrams; try to convince yourself that the situation depicted in each diagram offers one reasonable way to interpret the sentence’s meaning.
This will get more challenging as we move to sentence 3.
3. There are exactly two G3s [who talked to exactly two G2s [who talked to exactly two G1s]].
This sentence offers plenty to occupy our attention. I’ll start by exhibiting various situations which distinguish certain scope readings, in the sense that in the situation labeled by some scope reading that scope reading holds and no others do.

These diagrams, like before, are designed precisely to be true only under one particular scope reading. Again, I urge the reader to practice understanding scope by reading the sentence while looking at each of the three above diagrams. Try to understand, for each one, the sense in which that diagram depicts precisely one of the sentence’s possible scope orderings.
The reader will have noticed, by now, that I’ve only shown three orderings among the total possible six. There’s a reason for this. Here’s where things begin to begin to get very difficult.
The three scope resolutions I’ve depicted represent sensible interpretations of the sentence. These are the only ones with this property, though, and the other three orderings are incapable of producing meaning. It’s not that these other orderings depict meanings which are ridiculous — this has never stopped me — but rather that it’s impossible for me, and unless I’m missing something, for anyone, to assign a meaning to them. (I encourage the reader to try.) This fact, we’ll find, depends on syntactic features.
In general, only certain orderings of the numbers 1, 2, …, n represent admissible scope readings. We have:
Claim: Characterization of admissible scope readings. In any member sentence n of the above family, the admissible scope readings are precisely those obtained by taking some number i, i = 1, …, n, and reversing the order of the subsequence i > … > 1; that is, those sequences of the form n > … > i + 1 > 1 > … > i. These readings are semantically independent.
Let’s call the sequence n > … > i + 1 > 1 > … > i i-inverted. It follows from the above claim that sentence n has precisely n admissible scope resolutions, namely those corresponding to the the i-inverted sequences for each i = 1, …, n. Thus, though we’ve failed at Game 3, it turns out that we’ve accidentally offered a second, and roundabout, solution to Game 1.
The claim relies on a few observations, and the first part of its “proof” is best understood inductively. Firstly, observe that the “purely inverted” scope reading 1 > 2 > … i of the determiner phrase exactly two Gis … who talked to exactly two G1s is sensible. (One can become convinced of this by thinking about it; our above work on the 1 > 2 > 3 scoping is a good guide.) Next, observe that the scope reading obtained by couching a sensible reading into one extra embedding — and using the surface scoping between the old phrase and the new (i.e., letting the new determiner outscope all the old) — is itself sensible. (Again, think about it; use 3 > 1 > 2 as your guide.) Finally, observe that all sequences of the above form can be constructed using repeated application of the second procedure and possibly one non-trivial application of the first. Finally, to see why these readings are semantically independent, construct graphs like those shown above.
The converse statement holds that all sensible sequences are of the above form, or, in other words, that any sentence not of this form fails to convey meaning. Though I won’t prove this — I’m not even completely sure why, or that, it’s true — I’m convinced that this is where the deepest intrigue lies.
Recall that these sentences are also syntactically ambiguous, in the sense that one could bracket embeddings differently:
3′. There are exactly two G3s [who talked to exactly two G2s] [who talked to exactly two G1s].
(This means something very different, or rather it features its own scope ambiguities the set of whose resolutions’ meanings is disjoint.) As things stand, our sentences feature hierarchical embeddings. It would seem that the only legal scope inversions are those which completely reverse the scoping of the contents of a single syntactic embedding. It’s not possible, that is, to perform scope inversions which bring some determiner into higher scope than a determiner which itself both c-commands and linearly outscopes another. To do so would be to fail to respect a sentence’s syntactic structure, “slicing through” the contents of some embedding. Our property is accounted for syntactically.
I suspect that a family of sentences with different bracketing patterns would be subject to analogous limitations.
It looks like what we could use around here is some more complexity, right? In that vein, I must divulge that yet another attempt at treating Game 3 has fallen; I have already replaced it with an updated version. For the time being, I’m replicating here my (second) treatment of the game, and artificially backdating the comment to keep this at the top. Details about why exactly this treatment is incorrect will be provided below, in the comment thread.
Game 3: Construct a family of sentences 1, …, n, …, such that the nth sentence features n-2 non-trivially incomparable pairs.
Solution: Consider a collection of disjoint groups of people G1, G2, …, Gn, … and the following sentences (with embeddings bracketed to resolve syntactic ambiguity):
1. There are exactly two G1s.
2. There are exactly two G2s [who talked to exactly two G1s].
…
n. There are exactly two Gns [who talked to exactly two G(n-1)s [ … [who talked to exactly two G1s] … ]].
The somewhat contrived task put forward in this game relies on the scope readings available to these sentences, which we’ll now explore.
Scope relations take place between determiner phrases. Determiner phrases themselves consist of a determiner plus a noun phrase. Sometimes, this noun phrase itself features complex embedded subphrases. For example, consider the noun phrase
I propose the following tentative law:
Claim: Whenever a determiner phrase is used as a direct object, this determiner phrase must outscope any determiner phrases contained inside its own noun phrase.
This law will be illuminated throughout the investigation below.
Recall sentence n:
n. There are exactly two Gns [who talked to exactly two G(n-1)s [ … [who talked to exactly two G1s] … ]].
Which independent scope readings can we construct? We’ll work outward from the innermost phrase. Performing linguistic substitutions on each phrase’s direct object, we’ll find that the set of scope readings available to us is quite limited.
Start with the innermost phrase, who talked to exactly two G1s. This phrase has, as direct object, the determiner phrase exactly two G1s, with noun phrase G1s. Denoting G1 by A, the noun becomes simply A, and the phrase becomes the clearly unambiguous
The next-innermost phrase is who talked to exactly two G2s who talked to exactly two G1s. This phrase has as direct object a determiner phrase whose noun phrase is the slightly more complicated G2 who talked to exactly two As. There is only one scope interpretation of this simple noun phrase! Denoting this unambiguous noun by B, the next phrase yields the still-unambiguous
where a B, of course, is a G2 who talked to exactly two As.
By now, the pattern is clear. Each determiner phrase contains a noun which, on its own right, is unambiguous. Because the direct object’s noun can be replaced by a letter, all scope relations permissible within that noun must be resolved before its enclosing sentence can itself be given meaning.
Iterating this process, we produce a scope reading represented by the following logical expression (I informally use “∃2” to stand for “there exist exactly two”):
n. There are exactly two Gns [who talked to exactly two G(n-1)s [ … [who talked to exactly two G1s] … ]].
a. ∃2un[Gn(un) ∧ ∃2un-1[G(n-1)(un-1) ∧ talked(un, un-1) ∧ ∃2un-2[ … [G1(u1) ∧ talked(u2, u1) ] … ]]]
This reading’s independence is suggested by the following diagram, which depicts a possible real-life situation true of the reading given above and no others:
(A noun phrase’s scope relations must be resolved before it is used within a direct object.)
The argument carried about above, of course, doesn’t apply to the top-most phrase,
in which the key noun phrase, namely Gn who talked to exactly two Ms, is never used as a direct object and need not be resolved in advance. This phrase as a whole indeed is ambiguous, and here, finally, we may take the inverse scope relationship. This yields a second reading of sentence n, given by the following logical expression:
n. There are exactly two Gns [who talked to exactly two G(n-1)s [ … [who talked to exactly two G1s] … ]].
b. ∃2un-1[G(n-1)(un-1) ∧ ∃2un[Gn(un) ∧ talked(un, un-1)] ∧ ∃2un-2[G(n-2)(un-2) ∧ talked(un-1, un-2) ∧ ∃2un-3[ … [G1(u1) ∧ talked(u2, u1) ] … ]]]
This reading’s independence is asserted in the following diagram, which depicts a situation true of this reading and no others:
(This alternative scope reading inverts the topmost phrase.)
A careful reader might have noticed an oddity here. Why can’t we still proceed here as we did before, arguing that the sentence
— where an N is defined precisely as a Gn who talked to exactly two Ms — is unambiguous? I don’t know. This seems to be a strange instance in which substitution breaks down. It strikes me that something about the direct object “contains” scope in a way that the subject complement does not.
In any case, these two readings are available and independent in sentence n for each n ≥ 2.
The second of these two readings provides our first instance of non-trivial incomparability. Syntactically speaking, the determiner phrase exactly two Gis c-commands exactly two Gjs for any choice of i > j. In the first, scope, like c-command, is strictly linear from n on downwards. In the second, G(n-1)s outscopes both Gns and G(n-2)s, between which no scope relation exists.
The scope relations in the two respective readings are displayed in the following directed acyclic graphs, in which arrows point to higher scope, and non-adjacent arrows are omitted:
(The second partial order features incomparable pairs.)
In the second graph, incomparability relations occur between the pairs exactly two Gns and exactly two Gis for each i = 1, …, n-2. Because c-command is linear from n downwards, each of these incomparable pairs is non-trivial. By increasing n, we can freely control the number of such pairs.
We’ve demonstrated that there are two independent scope readings. Are there more? It would seem not, for reasons I’ve discussed above. In fact, it seems that embedding structures, particularly those linked to direct objects, limit scope flexibility in significant ways.
Sentences containing many determiner phrases either amass them laterally, say, through conjunctions and disjunctions, or hierarchically, through embeddings. Lateral constructions append siblings to existing nodes; embeddings introduce new children. In a way, lateral combinations are uninteresting. Adjacent siblings can’t affect each other, and the behavior of any (sub)sentence containing parallel phrases can always be reduced to that of its constituents. Embedded phrases, on the other hand, can (at least in principle) feature interesting scope interactions, and it’s in these that a sentence’s complexity lies.
Even in the second case, though, we find that the scope behavior is almost always limited to surface readings, especially in nodes lower in the syntax tree.
Another task for the reader: spot all of the scope ambiguities present in this post (aside from those in the example sentences).
Typical mathematician.
I would also note that you’ve assumed “talking” (as in Frenchmen talking to Russians) is something that can only happen between two people at a time. However, when I first read sentence 6, I just took it to mean “A group of 3 Frenchmen collectively talked with a group of 5 Russians”. This is something that might have happened at a bar in Napoleonic times, for example. This reading, of course, is independent from 6A and 6B, and doesn’t follow the same rules.
Other examples would include “3 Frenchmen shot at 5 tigers”, as you mentioned, or “3 witnesses talked to 12 jurors”.
Here, Park actually discusses the reading you bring up, with reference to the sentence I mentioned:
This conjunctive or cumulative reading is the one you’ve described. Park cites literature, we see, which argues that 20.b. has such a reading.
I did not intend to describe such a meaning. Perhaps I should have used a more explicitly one-to-one verb like “shook hands with”. It’s concerning, in fact, that I used sentences in which the cumulative reading is perhaps prominent in games for which the standardly scoped meaning instead was desired.
Nonetheless, it’s interesting that such a reading exists. Park describes more precise conditions under which a cumulative reading can be ruled out:
You’ve described another sort of reading over the phone, namely, the sort under which a sentence like “Three salesmen canvased two neighborhoods” would be true of a situation in which the combined work of three salesmen was sufficient to cover two neighborhoods. This is like the cumulative reading, and it might be linguistically classified as such. And yet to me it seems subtly different. Unlike that taken by the collectively shooting Frenchmen, the action taken by a salesman is individual, and the work of each salesman can be “modularized”. The sentence, meanwhile, refers to their combined action. This is different from the other readings we’ve dealt with.
I agree that the salesmen example seems distinct from the shooting at tigers example. The salesmen didn’t just “pepper” both neighborhoods with visits; they each methodically canvassed their assigned portion of the neighborhoods.
The salesman example, though, does remind me of my reading of another sentence: “Two fairies have talked with every Athenian”. When I first read this, I interpreted the sentence according to the cumulative reading, and that of the salesmen type: “Between both fairies, every Athenian has been talked to”. Compare this with: “Between the three salesmen, both neighborhoods were canvassed”. With the Athenians example, though, one could also take a “non-modularized” cumulative reading: “Both fairies, at one time, addressed every Athenian”. This reading is similar in intent to “Three Frenchmen shot at five tigers” and “Three witnesses spoke to the twelve jurors”.
So, it seems that we can produce both modularized and non-modularized cumulative readings of some sentences. These seem to be distinct in meaning, but I agree that they’re probably linguistically-equivalent.
A lovely choice of topic Ben, and nicely written to boot. Good stuff. I sympathise quite a bit with your fascination with possible readings as opposed to readings likely in natural English.
Just a few comments and appeals for clarification, though.
1. “Sentence 6.B. can be true while sentence 6.A. remains false, if, say, two distinct fairies visited each Athenian.”
I find your treatment here a tad confusing. 6.A. couldn’t possibly have a logical form which rules out its being true in the case that two distinct fairies are at issue, could it? The truth or falsity of the reading of 6.A. turns not on the distinctness of the two fairies (which is allowed by dint of the quantifier phrase ‘there are two’) so much as the particularity of the fairies. 6.A says that two particular fairies talked to each Athenian, whereas 6.B. simply says that each Athenian had two fairies talk to him – perhaps different pairs of fairies for different Athenians.
2. The sentence 7 is multiply ambiguous. Its non-inverse reading is ambiguous between (1) three particular Frenchmen visiting five particular Russians and (2) three particular Frenchmen each visiting a group of five Russians, where the set of groups of Russians is possibly pairwise disjoint. And 7’s inverse reading is similarly ambiguous.
3. “It’s not true, on the other hand, that each sentence’s various readings are completely semantically independent of each other in the sense that for any individual reading one can find a situation where this reading holds and no others do (or, equivalently, that this reading implies no others). In this particular family, in fact, to the contrary, it would seem to me that among the n scope readings (ordered by preservation of c-command relations, as above) of any given sentence n each reading implies the first and no others. (Recall that in sentence 4 above, which resembles sentence 2 here, 4.B implied 4.A.)”
First, note that, actually, 4.B. does not imply 4.A. Why would my believing of a mathematician that he wrote some book imply that I believe a mathematician wrote the book? Alice Liddell may have known that the charming Mr. Dodgson invented splendid tale for her and her sisters without knowing what his proper job was. In that scenario, 4.B. is true and 4.A. false. They are logically independent, as they stand. This, to logicians and philosophers is the well-known distinction between de re and de dicto scope readings. Second, and on the back of this last point, there is no straightforward logical connection between the nth sentence and its prior or subsequent fellows. The first sentence does not imply any of the remaining ones and no sentence implies any of its predecessors. (Why on earth would 3B imply 3A?)
4. “These are the only ones with this property, though, and the other three orderings are incapable of producing meaning.”
From what you’ve said, it seems to follow that, say, 1 > 3 > 2 is a scope reading incapable of having meaning assigned to it? Challenge accepted.
To be extra vivid in giving meanings, let’s replace, for the sake of the example, G1, G2, and G3 with Priests, Bishops, and Cardinals, respectively. Suppose the original sentence is ‘There are exactly two Cardinals who talked to exactly two Bishops who talked to exactly two Priests’. Then 1 > 3 > 2 gives a reading on which, for exactly two particular Priests there are exactly two Cardinals for each of which there are exactly two Bishops, such that each such Cardinal talked to each such Bishop who talked to each such Priest. (In the original notation, the diagram has two G1 spheres on the right in the largest size, four G3 spheres on the left in the medium size and eight G2 spheres in the middle of the smallest size. From each G3 sphere, two arrows points to distinct G2 spheres each of which has at most one arrow pointing to it(x) and each of which has exactly one arrow pointing to the same G1 sphere as the G2 sphere which is pointed at by the same G3 sphere that points to it(x). But no G1 sphere has more than four arrows pointing to it.) This seems a fairly coherent meaning to me. Again, a way of reading it is: There are two particular priests for whom exactly two cardinals talked to two Bishops who talked to them. Have I missed something? Or maybe I’ve just misunderstood you?
Once again, a great piece. Lovely topic.
Richard, good comments.
1. Yes, my terminology was unclear, and I’ve updated the piece accordingly. It should be better now. Perhaps unsurprisingly, it can be hard to resolve scope ambiguities using standard English even when one tries to.
2. I think you might be a bit off here. What you seem to have in mind is what we could describe as a complete bipartite graph between three Frenchmen and five Russians. And yet this does not represent a distinct disambiguation of the sentence, but rather a situation which is true under both disambiguations. Let’s try to be more precise. I suppose that what we mean when we say that a sentence, or perhaps rather a syntax tree, is scope-ambiguous is that it is representable by two or more nonequivalent logical expressions; when we say that a sentence is multiply ambiguous, we mean that it’s representable by three or more nonequivalent logical expressions. And yet this sentence — again, barring cumulative readings and using only “basic” notions of scope — has only two readings, or that is two possible logical expressions. Of course, there are (very) many real-life situations which might be true under one, or another, or both, or neither of these scope readings. The “complete bipartite graph” situation happens to be true under both. But this isn’t to say that it represents a distinct disambiguation, or that there exist more than two.
3. Yes, I was absolutely incorrect here, and I’ve updated the piece. Thank you for pointing this out. As a side note, I’ve noticed something amusing: Much of the terminology in this area seems well-suited for certain “simple” ambiguities and not for more complex cases. The distinctions between “surface and inverse” and between “de re and de dicto“, for example, only hold meaning, it would seem, with respect to the relative positions of precisely two operators/determiners/etc. What about when we have more than two? Which of the scope readings 3.A, 3.B, 3.C is surface/inverse/de dicto/de re? Who’s to say. At this point, we can only say something crazy like “some are more de re than others”. In fact, in this class of examples there’s a natural way to “totally order” the set of any given sentence’s scope readings by c-command preservation, and in this sense we can sort the readings by surface-ness. In other situations, even this luxury too might be absent.
4. This is the trickiest part, and, after much deliberation — both before I published this piece and after I read your comment — I think I’m forced to argue once again that this meaning isn’t furnished by the English. I spent much time thinking about these. In fact, the 1 > 3 > 2 reading occupied my attention above all the others before I published the post. Of course, the situation you’ve described is on its own perfectly coherent, and it is the obvious candidate for the scope reading’s viability. I think it fails, nonetheless. I’ll go into my thought process.
First, let’s make clear that we must fix the sytnax:
3. There are exactly two G3s [who talked to exactly two G2s [who talked to exactly two G1s]].
And we can’t allow:
3′. There are exactly two G3s [who talked to exactly two G2s] [who talked to exactly two G1s].
(I’ve bolded words for reasons I’ll make clear below.) The short version of my answer is that the 1 > 3 > 2 reading, and in particular the graph you’ve described, is tempting precisely because the reading does exist in English provided that we surreptitiously switch the syntax to that of 3′. The situation of 3′, though, is quite different; here, arrows connect G3s directly to G1s and there are no arrows between G2s and G1s. We must forbid ourselves from making this switch.
The first thing we should ask is to whom the who which I’ve bolded refers. In the 3′ syntax, it refers to the G3s, and this what makes that scope reading permissible: The G3s and G1s are connected 2-to-1 according to the inverse reading between them. In the 3 syntax, it refers to the G2s. We can imagine progressively constructing a sentence’s extension by traversing its syntax tree bottom-up, or perhaps more aptly, inside-out. (This was, basically, the technique of my “proof” of the claim above.) Before we even talk about G3s, we have two G2s talking to two G1s (inverse reading). This reading can only provide for a 2-to-1 connection, and yet in the 1 > 3 > 2 reading the connection is 4-to-1.
The reason that other readings do permit 4-to-1 connections is that the syntax permits it. Let’s take the example of 3 > 1 > 2. In this reading, when we connect the higher-scoped DP (i.e. 3) to the lower-scoped DP (i.e. 1) we’re actually connecting 3 to the big, bracketed subphrase of the sentence consisting of 1 > 2. But the reason that we can safely bracket off this subphrase is because it is itself a syntax subtree, and, building the sentence from the inside out, this subtree’s extension is already coherent and constructed before we make the attachment. To go back to 1 > 3 > 2, this reading forces us to bracket “There are exactly two G3s [who talked to exactly two G2s]” first. What we do we then attach to the lowermost-scoped DP 1? Our only choice is to connect the whole thing we’ve built to it, leading to 3′ and the 4-8-2 graph you described (but again with different arrows!). Hence the temptation.
In the 3′ syntax, this move is predicted possible by my theory, because here the 3 > 2 DP as a whole, which we can bracket together as we construct the sentence inside-out, doesn’t linearly outscope anything when we attach it invertedly to the 1 DP. But in the 3 syntax, we can’t treat 3 > 2 as a single DP because we have to bracket 2 and 1 together first. So instead we’re forced to lift 1 above the linear relation 3 > 2, which is illegal.
This is really complicated, and I don’t know if I have the conceptual tools right now to adequately articulate it.
By forcing a direct connection between the G2s and G1s (Bishops and Priests) — and focusing your linguistic intuitions on this subtree of the sentence — I hope you’ll be able to convince yourself that this reading in fact doesn’t exist. Either that, or I need to make some revisions to my theory.
More generally, it seems that I could try to develop a theory which relates a sentence’s syntactic features to the set of possible logical expressions which it represents. Surely someone’s already done this. Pretty fascinating though. If I were a linguistics student…
Also, I met Hintikka briefly once. At a philosophical logic conference in Europe. He was getting along. Certainly a big age. Actually he just died a few weeks ago. He was a philosopher whose chief trouble was having too many good ideas.
“My interest lies not so much in which readings are acceptable to English speakers as in how many readings we can create, acceptable or not.”
Correct me. You are working on the assumption that language use is a matter of processing meanings of words? A dictionary operation? We check words against related sets of words in our mental and cultural dictionaries and conceptual maps?
How about : language use is a matter of comparing underlying concepts against the real objects and object actions they refer to? In the real world?
So to process/understand CHAIR we check our concept against a real object example? Crucial if s.o. says HAND ME THAT CHAIR
And if we can’t physically do that, if we can only read IT IS THE MOST BEAUTIFUL CHAIR, we make a marker that that has to be checked out in the real world later if possible.
If language is basically REALITY CHECKING as opposed to LOGICAL/LANGUAGE CHECKING then the answer to your implied question is simple: there are *infinite* possible “readings” or to be more truthful “realisations” of any given concept. Because the real world affords evernew and potentially infinite forms of any given real object.
Keep it real, bro.
ikbol, thanks for the comment.
Maybe you can elaborate more thoroughly on the distinction you’re making.
When I ask about “how many readings” a sentence has, I’m asking about how many logical expressions this sentence represents. This is distinct from the question of “how many real-world situations” a sentence is true of. (I discuss this distinction in some detail under part 2. of this comment.) I think you might be mistaking the former for the latter.
Yes, any given sentence might be true of infinitely many possible real-world situations. But it might also have just a few scope readings, or only one.
Thanks again for your response.
AFAICT you’re taking a standard linguistic approach to language which is to see it as logical – as having determinate meanings – just as logical expressions have determinate meanings. The ideal language, pace Wittgenstein, would have only one meaning per word – and pace most people in AI/NLP. That’s the ideal, even if not practically possible, helas.
In fact, language is the OPPOSITE of logic. Logic and maths have VARIABLES which have specific sets of meanings. They can’t really handle CONCEPTS at all.
Concepts can’t and aren’t meant to have meanings. Every concept in language is creative and has actually evernew and potentially infinite real world referents -as CHAIR does. To talk about language having specific MEANINGS is to be completely divorced from the reality of language use. In real world language use, as distinct from the fantasy world of most linguistics, for example, any given text, if popular, has a fast-approaching-infinity of actual INTERPRETATIONS. Take Hamlet, the Bible, Obama’s latest speech… People will never agree precisely, logically about any text’s or even sentence’s “meaning.”
So the challenge in understanding how language works, is to understand how the concepts of which it consists, are infinitely adaptable to real world referents – how you are able to HAND ME THAT KNIFE for ever diversifying examples of knife, or GO THROUGH THAT ROOM for every diversifying examples of room.
No logic-based program can *begin* to do this, They can only deal with specific knives and rooms. This is the unsolved problem of AGI – to be able to handle an evernew, everdiversifying world via the creative concepts underlying language.
The creative nature of language’s concepts means that you and I/ different people can agree in a loose general way about whether you have GONE THROUGH THAT ROOM or HANDED ME A KNIFE – even though our individual ideas/protoypes of KNIFE/ROOM are almost certain to be considerably different.
Logic, maths and algorithms cannot and never will be able to understand how concepts work. We need a totally different approach.
ikbol, thanks again for your thoughts.
I agree with you. Language is fluid, and the “logical approach” is very restrictive — and doesn’t reflect the realities of language use. I’m reminded of this comic.
Nonetheless, we may still pick small, controlled subsets of our language — subsets which lie rather close to the “variables” side of things — and study how these controlled systems operate. We’re selecting a small part of language, choosing fixed, unambiguous rules for it, and, in a way, formalizing the whole thing. Then we study it as a formal system.
The study of this formal system, though, is constrained in very real ways by intuitions which come from our practical, everyday use of the language. We use language’s reality to study its formalization. This was very evident in my study: not all formal possibilities were permitted by the constraints of everyday use. Linguists too, famously, use native speakers’ grammaticality judgments in their experiments. The reason we must adopt strict formal rules for the subsets of language we study is so that we can clearly articulate which of its features are indeed acceptable under everyday language usage rules. This is largely what linguistics does, particularly in the subfields of morphology, syntax, and semantics.
You could argue that the techniques inherent in linguists’ formalizations have no basis in linguistic reality. And yet this would seem to deviate from the facts. Linguistic conclusions about the features necessary and sufficient for grammaticality — these features are expressed in formal terms, recall — have proven extraordinarily predictive in future grammaticality judgments. This is because the descriptions of the rules, as well as the particularities of the formalizations, coincide with real language usage.
It’s true that this formalization leaves much unaccounted for. It fails to account for large swaths of the breadth of ways that people use language. Language use is extremely subtle, as you rightly point out. At the same time, however, this is partly the point. Linguistics only sets out to study certain things, and not all things. Semantics in particular, for example, famously studies only entailment relations between sentences, and not the truth value of individual sentences themselves. This is because the truth value of an individual sentence depends on pragmatics, or usage. Semantics can’t account for that.
The separation is extremely useful. It allows semantics to do its work where it can, and step aside where it can’t. This article, in particular, was a study in semantics.
For example, from the syntactic, and even perhaps semantic, point of view, two sentences like “That man is male” and “That man is just” are probably quite similar. And yet the latter is very challenging from the pragmatic point of view.
Pragmatics, in linguistics, studies language use, and this might be closer to what you’re thinking about. You should remember nonetheless, though, that other subfields of linguistics, like semantics, choose not to ask these questions — and for good reason. To study semantics, we have to agree on usage rules. Restrictiveness aside, semantics has been a highly successful field.
I’m here to stir things up and declare much of what’s been said to be wrong. Or, at least, I intend to put it in question. This entire endeavor risks becoming pseudoscientific, since we seem to be making claims that we can’t really verify, and, more importantly, don’t have the tools to verify or don’t know what those tools are. So, rather than make claims that aim to be definitive, I seek to just improve understanding of the task at hand.
Firstly: I certainly believe that 3 > 2 > 1 is valid and sound. Once again, we have the sentence:
3. There are exactly two G3s [who talked to exactly two G2s [who talked to exactly two G1s]].
As an exercise, let’s make some substitutions. Let an A be equivalent to a G2 who talked to exactly two G1s. Now, we can safely and comfortably say that “There are exactly two G3s who talked to exactly two As” [by surface reading]. We could then say that a B is equivalent to a G3 who talked to exactly two As”. We could, again, rephrase question 3 as “There are exactly two Bs”. It would be easy to keep building, starting with “There are exactly two G4s who talked to exactly two Bs” [by surface reading].
I think these substitutions constitute a valuable tool. Some sentences won’t work well with substitutions, but others might.
Let’s turn towards 1 > 2 > 3. We can’t make any substitutions here. This might tell us that inverse readings aren’t as amenable to nesting as we’d like them to be.
I argue, firstly, that the right panel of image 3 does not represent any possible reading of sentence 3, and secondly, that a 1 > 2 > 3 reading of sentence 3 is impossible altogether.
First, let’s show that the right panel doesn’t represent sentence 3. For sentence 3 to obtain, two G3s have to talk with exactly two G2s, whether by surface or inverse reading. But neither reading results in what’s shown in the right panel. By the surface reading, we would have each G3 talking with two G2s. The inverse reading, on the other hand, would entail a total of two G2s, each of which is talked to by two G3s. Neither of these is occurring in image 3 right panel.
The only way to describe the right panel with inverse readings would be to break the sentence up. Using only inverse readings, we could successfully say of the right panel that “Two G3s talked with four G2s [by inverse reading]. Meanwhile, Two G2s talked with two G1s [by inverse reading]”. What we’ve really done is describe the right panel with a 2 > 3 reading and then with a 1 > 2 reading.
Now, I’ll explain why it’s impossible to create a single-sentence 1 > 2 > 3 reading of sentence 3.
Another way to write sentence 3 would be to say “There are two G3s who talked with two G2s. Those two G2s talked with two G1s.” The word WHO ensures that this is the case.
So, in sentence 3, by the 1 > 2 > 3 reading, we have that “Two G3s talked with two G2s” [by inverse reading], and that “THOSE SAME TWO G2s talked with two G1s” [by inverse reading]. But the latter sentence is impossible. In order for two G2s to talk with two G1s by inverse reading, we need FOUR G2s. So, with only two G2s doing the talking, the inverse reading cannot hold.
Thus, a 1 > 2 > 3 reading of sentence is wholly impossible. The relationship described between G2 and G1 cannot possibly hold, since we’re told right off the bat that only two G2s are acting, and we need four.
If you believe what I’ve written so far, you’ll be able to find on your own that the 3 > 1 > 2 and 1 > 3 > 2 readings can’t stand. But I’ll try go over them myself briefly.
The 3 > 1 > 2 panel has problems including those I’ve described, and more. Firstly, let’s consider G1s and G2s only. Regarding the middle panel of the image, it’s certainly not the case that two G2s talked with two G1s, by inverse reading. Rather, two G2s talked with FOUR G1s by inverse reading. So, we already know that this middle panel cannot be representative of sentence 3. Further, the relationship between G3s and G2s depicted in the middle panel also fails to satisfy the surface reading. Rather, two G3s are talking with four G2s [by surface], not two.
Can we create an accurate 3 > 1 > 2 reading? We run into the same problem as before. We have that “Two G3s talked with two G2s” [by surface reading] and that “THOSE SAME TWO G2s talked with two G1s” [by inverse reading]. Once again, we only have two G2s to work with, but we need four to create the desired inverse reading. So, we have the same problem as before: it takes four G2s to satisfy the inverse reading of “Two G2s talked with two G1s”, not two. In the 1 > 2 > 3 case, the G3-G2 relationship produced four G3s and two G2s, so we knew right away we wouldn’t have enough G2s to allow the G2-G1 relationship to work. In the 3 > 1 > 2 case, the G3-G2 relationship produces two G2s and four G2s, which is enough parents for the G2-G1 relationship to work. However, this still doesn’t change the fact that we’re told that the G2-G1 relationship is fulfilled using only two of the four G2s produced by the G3-G2 relationship, again because of the word who.
Richard, I copied down the chart you describe, and I don’t think it works. Let’s first consider the relationship between priests and bishops, which is supposed to satisfy an inverse relationship. It’s not the case that exactly two bishops spoke to two priests [by inverse reading]; rather, FOUR bishops spoke to two priests [by inverse reading]. Now, cardinals and bishops were supposed to follow a surface reading. But, it’s not the case that two cardinals spoke to two bishops [by surface reading]; rather, FOUR cardinals spoke to two bishops [by surface reading]. It’s true that for each priest there are two cardinals and for each cardinal two bishops, and that cardinals talk to bishops who talk to priests, but this isn’t sufficient to satisfy the demands of the 1 > 3 > 2 reading.
Interestingly: 2 > 1 > 3 holds! Actually, I’m not really sure how this a > b > c notation works, but: If the relationship between G2 and G1 is surface and the relationship between G3 and G2 is inverse, we can create a working interpretation of sentence 3. One key fact regarding this sentence is that we can substitute with A. So, we can write: Two G3s spoke with two As [by inverse reading]!
I think we may be finding a pattern: the ability to substitute is key. We could also say, for example, that “Two G4s talked with two Bs” [by inverse reading]. So, allowed readings are:
3 > 2 > 1;
4 > 3 > 2 > 1;
2 > 1 > 3;
3 > 2 > 1 > 4;
n > n-1 > … > 1;
n-1 > n-2 > … 1 > n.
The key point is that, if we wish to create a relationship between Gs which uses the inverse reading, that reading must occur FIRST. That’s because, surface readings are flexible. They mandate that each PARENT has two CHILDREN, for ANY amount of parents. This allows us to easily make nesting substitutions. Inverse readings, on the other hand, are more restrictive. They mandate not only that each CHILD has two PARENTS, but also that there are two CHILDREN. Thus, there must be FOUR parents. And, as we’ve seen earlier, we can NEVER see an inverse relationship AFTER a surface one, since ALL surface relationships beget only two children per node, and it’s these TWO children that we’re left to work with in the production of the next inverse relationship. And, as said before, inverse relationships must have four parents, not two. Of course, we’re allowed to have a 1 > 2, and we’re always allowed to START with an inverse relationship, because it’s only in these cases that no children have been produced yet, so we’re allowed to start with the only number we’re allowed to start with: four.
I’m going to have a think about all of this and issue a statement soon, as soon as I get the chance.
Josh, this comment is largely in response to things you’ve said. But it’s sufficiently general that I’m putting it in the top-level feed.
I think it’s become apparent by now that this post, or at least the section under Game 3, is sufficiently in disarray that to attempt to re-write the post would be unfeasible. I’ll have to let it stand. I think that we’ve come far enough now, though, that I can start more coherently talking about what went wrong.
I’ve become convinced by your arguments, Josh, that the 1 > 2 > 3, 3 > 1 > 2, and 1 > 3 > 2 readings — or, rather, the diagrams we’ve used to represent these them — can’t stand. These situations simply aren’t true of the English, for reasons you point out.
The segment in dashes of the above sentence hints at an important mistake. (By to distinguish a scope reading I’ll mean to construct a situation or diagram of which this reading, and no others, are true.) Your arguments actually that the diagrams by which we’ve attempted to distinguish these readings fail to do so — indeed even to be true of the sentence. But does that mean that these readings aren’t given by the English?
I have in mind one argument, true or not, which seems to suggest that they aren’t. If a reading, a > b > c, say, were given, then I know what its logical expression “should” look like. Something like:
∃2x [ Ga(x) & ∃2y [ Gb(y) & ∃2z [ Gc(z) & talked(–, –) & talked(–, –) ] ] ]
(I’ve left the arguments of talked blank because I don’t know the correspondence between a, b, c and 1, 2, 3. In some expressions, one of the talked predicates could be lifted to a higher scope.)
Supposing that the a > b > c scope reading indeed must take such a form, it would seem that we must be free to choose whichever arrangement we’d like that satisfies the expression. The ones I chose above surely do. That these don’t work doesn’t seem to bode well for the viability of the scope reading in general.
Could it be the case that a reading is present in the English, and yet that it’s impossible to construct a situation which distinguishes it? This is a strange possibility. This readings would be inaccessible. Take the real-world situation with exactly two G1s, exactly two G2s, …, and exactly two Gns, in which the graph between the pair of Gis and G(i+1)s is complete bipartite for each i = 1, …, n-1. This situation would be true of just about any scope reading I could come up with. Does this mean that all scope readings are “given”? I’m not sure. It might depend on what we mean.
As my friend Rachel said, “This starts getting into the question of what natural language is.” I’ll try to recall her arguments. The condition of being “part of the language” is grounded first and foremost in native speaker judgments. These are the “data”. Linguists’ theories purport to explain and predict native speaker assessments. These theories are grounded in intrinsic or formal properties of the sentence. We can take these theories and extend their predictions to sentences much larger than those over which they were originally intended to preside — sentences which would be rejected by native speakers. The conclusions these theories elicit in this setting, though, can only be said to comprise some sort of “generalized English”, and further the “generalized English” we land on will depend on the theory we choose. To say of a reading that it is “in the language” implicitly presupposes a linguistic theory. Given a choice of theory, moreover, a reading’s subsequent “grammaticality” might be better understood as nothing more than a formal consequence of the theory.
These are interesting points. I might respond only with a few things. For one, I would guess that these theories are pretty consistent in their judgments — especially for sentences which, like these (purposefully), are somewhat regular by construction — and that our various “generalized English”s might not differ by too much. A second independent point is that language and grammatical sentences feature substantial underlying regularity and that these theories perhaps pinpoint fundamental intrinsic properties of sentences which are robust on generalization to larger sentences. In other words, the “locus of truth” for grammaticality judgments can be safely shifted from empirical native speaker data to a sentence’s intrinsic structural properties. These latter properties, of course, generalize more easily. Moreover, the conclusions they’ll make regarding larger sentences are just as non-arbitrary as the conclusions they made for smaller ones. Grammaticality is an intrinsic property, and native speaker judgments simply reflect its presence. Finally, I would argue that the grammaticality we’re grasping for is more than formal. When we’ve found a meaning — modulo my false judgments — these have been meanings really graspable by our intuitive linguistic faculties. These sentences still are accessible. Of course, I’d like the help of a formal theory to sort out when, and why, readings fail to exist. But I would compare this theory’s output with my linguistic intuition.
These points lead to the conclusion that we can safely pick a theory and apply it to these sentences. Hell, let’s take multiple ones and compare their conclusions.
I’ll get back to this situation. Joshua, I do think that you’ve found new readings, or rather distinguished them. The family of diagrams you’ve described seems to uncover something new. Consider the groups G1, G2, …, Gn, each with, respectively, 4, 2, 4, …, 2^(n-1) members, connected in the obvious way. The crazy part, though, is that I think they can only be explained by a non-linear scope order. To quote myself:
I think this basic assumption has been unravelled. I think that, in the sentences you’ve described, we have the following scope ordering:
> 3 > 4 > … > n
2
> 1
We have a rudimentary tree. This is a partial order; in particular, there is no relation between 1 and, say, 3. Notice how this ordering is also reflected in the sizes of the constituents from each group: Each group Gi has 2^(n_i) members, where n_i is the depth of node i in the tree which represents the scope orderings. This is partly because your diagram is “maximal”, as the ones I tried to make were.
This hypothesized scope ordering is also reflected in the reading’s logical expression. I think it would look something like this:
∃2x [ G2(x) & ∃2y [ G3(y) & ∃2z [ … ] ] & ∃2z [G1(z) & talked(z, x) ] ]
Notice how there is a deep bracket consisting of the G3s, G4s, …, Gn. All of these scopes are closed, and then a new one is opened, containing only G1. Finally, this scope too is closed, and only then is the topmost scope closed. G1 and G3 actually operate on the same scope. They’re conjoined by an &, and neither one outscopes the other.
This seems to show that scope orderings need not be linear. This opens the possibility of a huge number of scope arrangements.
What do you all think?
Alright, some huge progress here. I rewrote the entire Game 3 to reflect some of these developments.
Joshua, I think you successfully identified the two readings you, and then I, described above as the two readings actually available in Game 3. Your linguistic intuitions took you to the finish line. But I think your ex post facto explanation for why gets things wrong.
You base the impossibility of many of these readings on questions of quantity:
But I don’t think quantity is what’s at stake here. I can construct a situation about which the inverse (and not the surface) reading of Exactly two G2s talked with exactly two G1s holds which uses only two G2s. See the picture below:

And yet it still seems impossible to put G3 under G2-G1 when we take this inverse reading in the latter. A successful account of the impossibility of the “purely inverse” reading must, it seems, invoke other arguments.
In my analysis, I take the mitigating factor to be the use of a noun phrase in a direct object. When a determiner phrase is a direct object, it can’t be outscoped by the determiner phrases in its own noun phrase (see above). Interestingly, (example shows that) this can happen when the determiner phrase is a subject complement.
It’s tempting to, as you did, tap the complementizer who as a significant factor here.
We even see this in the Stanford Encyclopedia of Philosophy, which has an incredible article about ambiguity:
SEP acknowledges that certain quantifiers can escape even relative clauses, despite the latter’s reputation as “scope islands”. Indeed, it seems like the presence of relative clauses is not what accounts for the scope inflexibility we observe here. After all, in
the quantifier exactly two has no problem escaping from the relative phrase who talked to exactly two G1s. I think we need (something like) my theory to account for the inflexibility here.
Alright, let’s begin the substantial task of debriefing from all of the comments above. It looks like we got a few things wrong. I’ll get to that in a second.
But first, the good news: while we were bad at deciding which readings are not available—the only if direction, so to speak—we were good at the if direction, which involved describing acceptable readings. In fact, we (Josh and I) were both right! Indeed, the final, or should we say general, treatment currently up for Game 3 contains both of our original postulates as special cases.
As I don’t have access to a pen and paper right now, I’ll try to spell the whole thing out in words. My original treatment of Game 3 (see the top comment) postulated as admissible exactly the “i-inverted” sequences; in our new terminology, these are represented by those graphs which consist of a single diagonal segment on the far right followed by a horizontal segment finishing out the graph; though these are certainly not the only available readings, they are permitted under the new theory. Josh, your original proposal deemed as acceptable only those scope readings whose graphs are either completely horizontal (“pure surface”) or completely horizontal except for a single node dangling diagonally from the left-most node in the horizontal streak. These too, of course, don’t exhaust the available readings, but again they’re both allowed.
And indeed, both of our arguments about why these were the only acceptable readings were fallacious (not that my current argument is much clearer—but I think it’s right, at least).
Interestingly, my rather cryptic statement in the original treatment that “It’s not possible… to perform scope inversions which bring some determiner into higher scope than a determiner which itself both c-commands and linearly outscopes another”, though confusing, seems correct. In fact, this is perhaps exactly a roundabout articulation of condition 1. of Claim 2 above. On the other hand, I was caught up at the time in my conviction that “the number of conceivable scope readings will correspond to the number of ways of ordering this total collection of determiners”—that, in other words, only total orderings of the determiners were permissible. Interestingly, the class of i-inverted sequences picks out exactly the class of scope readings which are admissible under the new theory and feature a total, as opposed to a partial, order on their determiner phrases. In other words, modulo an undue restriction to total orders, I got it right.
Of course, partial orders must be considered, and, Josh, this is where your insights come in. The myth of the necessarily total order was shattered by your comment here; unfortunately, you didn’t go far enough, and cut off a few avenues while you were at it. I don’t want to dive too deeply into what you got wrong, but I will make a few short statements. Central to your argument was a sort of “substitution” process: that to understand the sentence
it’s enough to call a G2 who talked to exactly two G1s an A, understand the phrase A (which happens to be unambiguous), and then finally understand the sentence
Yet this is clearly wrong on its face, for both A and the sentence above are unambiguous, while the sentence of the first blockquote is not.
Indeed, the first sign of trouble was visible already in my second treatment (see the second comment above), when I remarked that “Why can’t we still proceed here as we did before, arguing that the sentence…”. The key, though, is that the breakdown of the substitution process that I observed there is the rule, and not the exception, as we can see here. In fact, whether the sentence’s finite verb is a transitive or linking verb makes, contrary to my claims, no difference whatsoever, as even the sentence
is ambiguous, for the same reasons as before (and despite what substitutions may suggest).
What is wrong with the substitution argument? Well, essentially, (and crucially, one must follow it all the way to its conclusion, as I failed to do in my second treatment) it secretly claims that scope ambiguities don’t exist! Indeed, by resolving the scope relations of the c-commanded phrase before passing to an enclosing phrase, one tacitly prohibits the raising of any quantifiers in the c-commanded phrase out the gate. The whole reason scope ambiguities are tricky is that we can’t semantically analyze our sentences in this purely “local” way.
Furthermore, Josh, I think your claims about quantity (“two” and “four” and so on) are misguided. I already deflated a few of these in my comment here, so I won’t say much more about this. I’ll remark, though, that the whole point of reversing (or changing) the order of quantification is that you can’t put naive faith in the numbers you see written on the page in the order you see them, or more generally, after resolving only one of a sentence’s multiple ambiguities. This is related, in fact, (and maybe not surprisingly) to your claims about substitution. Just to give a simple example, to return to the standard sentence
it would be a mistake to start squabbling “but there were supposed to be two G2s; I see it written right there!” This is presupposing that the order of quantification is not reversed, which is exactly what is at stake. Of course, you make the claim with regard to sentence 3, but you make a similar mistake: you try to resolve the scope relation between the outermost two phrases first, and then make claims about the innermost. But this is not how sentences’ meanings are assembled. This is exactly the what we just saw in the sentence with two determiners.
To add a final note, by the time of my last comment I had already handled a few of these claims, and I concluded by suggesting “I think we need (something like) my theory to account for the inflexibility here.” What gives? Well, my theory was false—but so was the “inflexibility”, and there was nothing to “account for” to begin with. Problem solved.